Avant de quitter la Seine-et-Marne, on va parler encore une fois d’une découverte française. Cette fois, ce sera l’ingénieur Léon Charles Thévenin, de Meaux, qui étudiait les circuits électriques. Ce n’est pas un blog sur l’ingénierie électrique, et peut-être plus important, j’ai suivi mon dernier tel cours en 1997, alors j’essaierai de vous donner l’idée de façon simple. Mais Thévenin à découvert une idée pour rendre les circuits plus faciles à comprendre. On va parler de l’idée grosso modo sans maths.

Connaissez-vous la loi d’Ohm ? Ça donne la relation entre la tension et le courant dans une résistance. Les résistances sont les éléments les plus simples dans un circuit électrique parce qu’ils ne changent rien quant au temps. On va sauter ça et parler strictement de résistances. La relation découverte par Ohm est :

R = U / I

ou R est la résistance, U est la tension, et I est l’intensité du courant. Alors, considérez un circuit très simple, avec une source de tension et une résistance :

Si la tension est 240 volts, comme en France, et la résistance est 240 ohms, il y aura un courant de 1 ampère à travers la résistance. Vous êtes toujours avec moi ? Continuons.

Thévenin connaissait deux autres lois aussi, celles de Kirchhoff. La loi de nœuds de Kirchhoff dit simplement que n’importe où que l’on trouve un nœud, comme ça :

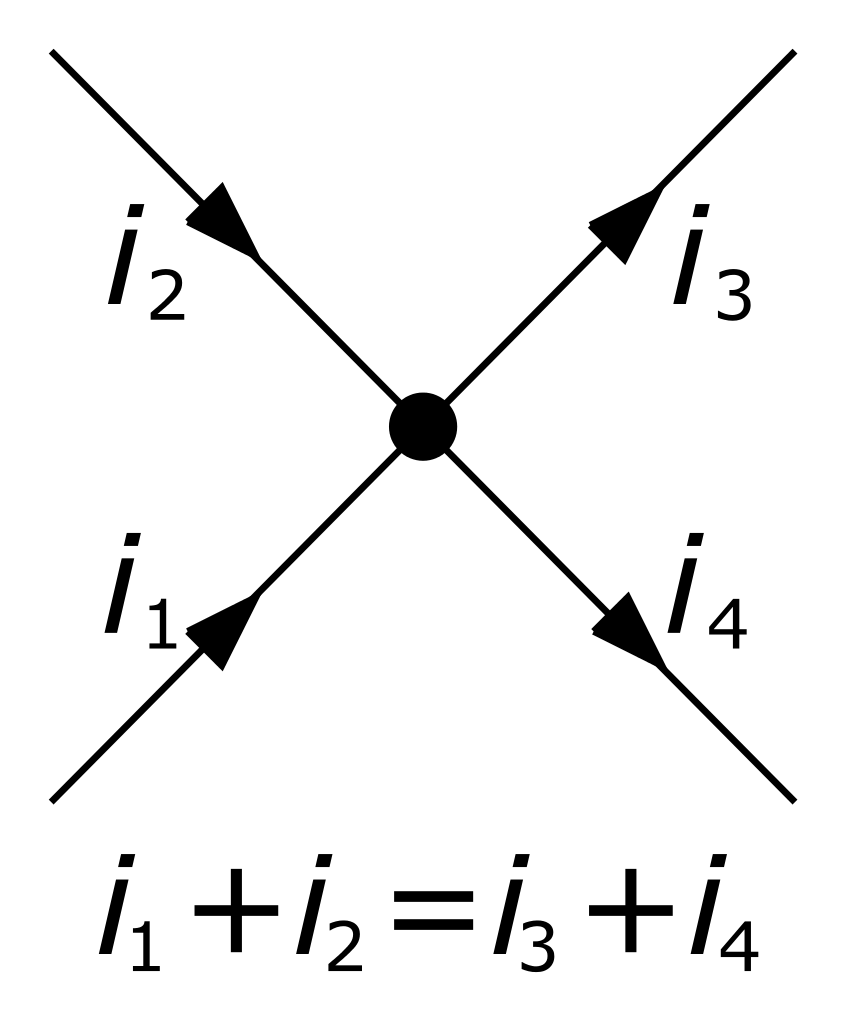
L’intensité des courants qui entrent le nœud est égale à l’intensité des courants qui sortent du nœud. Il n’est pas le cas qu’ils seront tous égaux. C’est la somme qui sera la même — si vous pensez à la loi d’Ohm, une résistance qui est 2x une autre resistance expérimentera une intensité de courant 1/2 le deuxième donnée la même tension. Mais s’ils touchent le même nœud, la somme des courants à travers les deux sera la même que le courant que le nœud a reçu.

La loi des mailles de Kirchhoff est similaire. Ça dit que dans un circuit électrique comme celui-ci :

la tension à travers la source (V4 ici) sera égale à la somme des tensions à travers toutes les résistances individuelles (V1 + V2 + V3). Comprenez-vous ce qui veulent vraiment dire les lois de Kirchhoff ? Dans un circuit électrique idéale — sans pertes réelles — rien ne change en total. On peut ajouter tant d’éléments que l’on veut, et les sommes ne changent pas, juste les valeurs mesurées par ici et par là.

Thévenin a bien compris ces lois. Alors sa grande idée, c’était que l’on pouvait remplacer un circuit, quel que ce soit, par un seule et unique générateur de tension et une seule résistance. Je ne vais pas vous mener dans un exemple, car il y a plusieurs manières d’ajouter les résistances, et ce n’est pas un blog de maths. Mais par exemple, on peut remplacer tout un schéma de 4 résistances par une seule et unique résistance, comme ça :

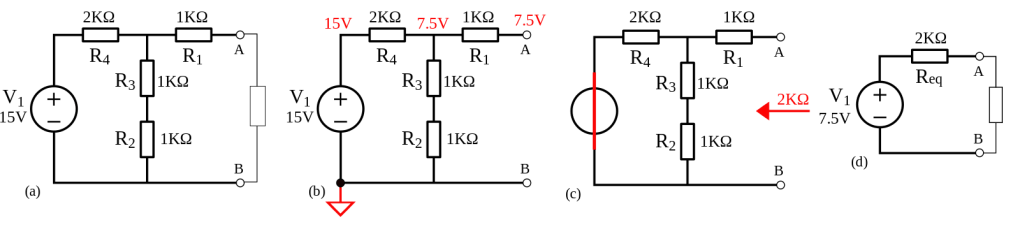
Évidemment, le schéma à gauche est beaucoup plus compliqué que celui à droite. Ça marche parce que l’on sait que la somme des tensions restera la même, et c’est le même pour les nœuds, qu’il y aura finalement la même intensité de courant.

Pourquoi donc avoir des circuits qui ne sont pas les plus simples ? La réponse, c’est qu’il reste d’autres fonctionnes pour les éléments du circuit. Par exemple, si vous voulez jouer un CD, ou bien un fichier MP3, l’électricité sera converti de forme numérique en forme analogique avec un réseau de résistances très similaire au circuit à gauche. (Il y a d’autres manières possibles ; laissez tomber, les ingénieurs.) On ne peut pas complètement nous débarrasser de circuits compliqués. Mais si on veut savoir combien de pouvoir électrique sera consommé par le réseau de résistances, on peut trouver l’équivalent Thévenin, et on le saura vite. (Sinon, on met des Linky partout. Je dis ça, je dis rien.)