Avant de quitter la Seine-et-Marne, on va parler encore une fois d’une découverte française. Cette fois, ce sera l’ingénieur Léon Charles Thévenin, de Meaux, qui étudiait les circuits électriques. Ce n’est pas un blog sur l’ingénierie électrique, et peut-être plus important, j’ai suivi mon dernier tel cours en 1997, alors j’essaierai de vous donner l’idée de façon simple. Mais Thévenin à découvert une idée pour rendre les circuits plus faciles à comprendre. On va parler de l’idée grosso modo sans maths.

Connaissez-vous la loi d’Ohm ? Ça donne la relation entre la tension et le courant dans une résistance. Les résistances sont les éléments les plus simples dans un circuit électrique parce qu’ils ne changent rien quant au temps. On va sauter ça et parler strictement de résistances. La relation découverte par Ohm est :

R = U / I

ou R est la résistance, U est la tension, et I est l’intensité du courant. Alors, considérez un circuit très simple, avec une source de tension et une résistance :

Si la tension est 240 volts, comme en France, et la résistance est 240 ohms, il y aura un courant de 1 ampère à travers la résistance. Vous êtes toujours avec moi ? Continuons.

Thévenin connaissait deux autres lois aussi, celles de Kirchhoff. La loi de nœuds de Kirchhoff dit simplement que n’importe où que l’on trouve un nœud, comme ça :

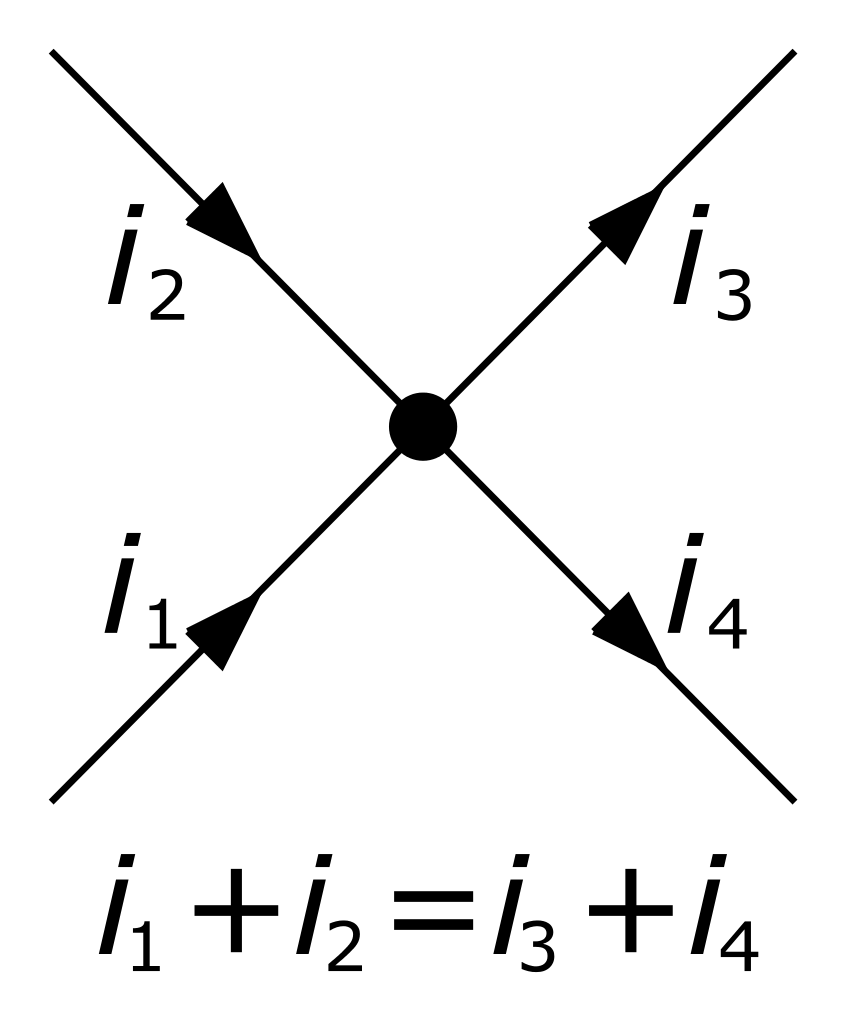
L’intensité des courants qui entrent le nœud est égale à l’intensité des courants qui sortent du nœud. Il n’est pas le cas qu’ils seront tous égaux. C’est la somme qui sera la même — si vous pensez à la loi d’Ohm, une résistance qui est 2x une autre resistance expérimentera une intensité de courant 1/2 le deuxième donnée la même tension. Mais s’ils touchent le même nœud, la somme des courants à travers les deux sera la même que le courant que le nœud a reçu.

La loi des mailles de Kirchhoff est similaire. Ça dit que dans un circuit électrique comme celui-ci :

la tension à travers la source (V4 ici) sera égale à la somme des tensions à travers toutes les résistances individuelles (V1 + V2 + V3). Comprenez-vous ce qui veulent vraiment dire les lois de Kirchhoff ? Dans un circuit électrique idéale — sans pertes réelles — rien ne change en total. On peut ajouter tant d’éléments que l’on veut, et les sommes ne changent pas, juste les valeurs mesurées par ici et par là.

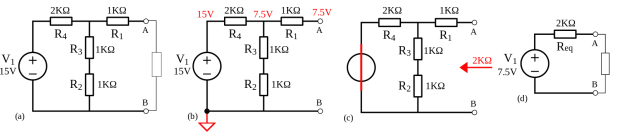
Thévenin a bien compris ces lois. Alors sa grande idée, c’était que l’on pouvait remplacer un circuit, quel que ce soit, par un seule et unique générateur de tension et une seule résistance. Je ne vais pas vous mener dans un exemple, car il y a plusieurs manières d’ajouter les résistances, et ce n’est pas un blog de maths. Mais par exemple, on peut remplacer tout un schéma de 4 résistances par une seule et unique résistance, comme ça :

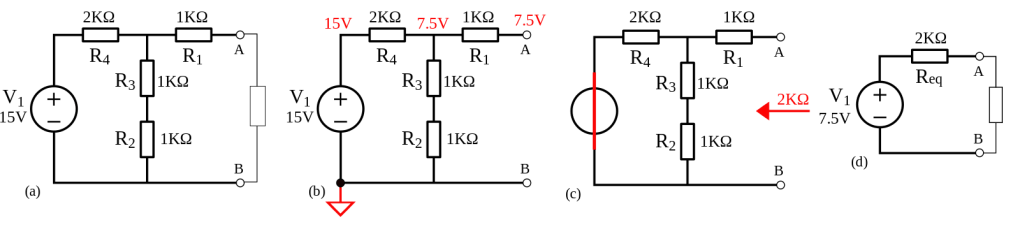
Évidemment, le schéma à gauche est beaucoup plus compliqué que celui à droite. Ça marche parce que l’on sait que la somme des tensions restera la même, et c’est le même pour les nœuds, qu’il y aura finalement la même intensité de courant.

Pourquoi donc avoir des circuits qui ne sont pas les plus simples ? La réponse, c’est qu’il reste d’autres fonctionnes pour les éléments du circuit. Par exemple, si vous voulez jouer un CD, ou bien un fichier MP3, l’électricité sera converti de forme numérique en forme analogique avec un réseau de résistances très similaire au circuit à gauche. (Il y a d’autres manières possibles ; laissez tomber, les ingénieurs.) On ne peut pas complètement nous débarrasser de circuits compliqués. Mais si on veut savoir combien de pouvoir électrique sera consommé par le réseau de résistances, on peut trouver l’équivalent Thévenin, et on le saura vite. (Sinon, on met des Linky partout. Je dis ça, je dis rien.)

On retourne vers les découvertes françaises avec un œuvre du mathématicien Jean d’Alembert, sa célèbre règle pour les séries. Ceci est loin d’être son travail le plus important, mais il n’y aura jamais de maths trop compliqués sur ce blog. Je ne veux pas perdre de temps en typographie pour les équations aux dérivées partielles non plus. Or, elle reste une avancée importante dans l’analyse numérique. Je suis ici l’exposition de Wikipedia en anglais car : 1) celle en français n’est pas suffisante, et 2) je suis trop paresseux pour inventer mes propres exemples.

Quelle est une série ? ([Quelque chose que vous regardez chaque semaine sur TF1 ? — M. Descarottes]) Pour une fois, notre ami a tort. C’est une séquence de numéros que l’on peut exprimer par une formule, et d’habitude on veut connaître soit la somme soit le produit. Ici, on parle seulement des sommes. Voici un exemple :

Comment lire cette série ? Ici, la variable n va de 1 jusqu’à l’infini, comme ça :

Un fait bien connu chez les mathématiciens est que ceux qui étudient l’infini deviennent souvent fous, comme Georg Cantor ou Kurt Gödel (deux de mes héros, au fait). Moins connu est qu’acheter de la vanille accélère le processus. De toute façon, pour chacun de ces nombres, on calcule la valeur de la formule. Pour nos buts, e = 2.71828 ; c’est un numéro très important dans les maths. Alors pour n égale de 1 à 3, c’est :

Ce n’est pas une grande somme, et on peut voir que les numéros en bas augmentent vite. (C’est bien connu que eⁿ va a l’infini.) Alors, on peut soupçonner que cette somme n’est pas infinie. Mais en tant que mathématiciens, on veut le prouver. C’est ici où la règle de d’Alembert s’applique. Il a reconnu qu’il y a une relation entre les termes au-delà de la formule.

Brièvement, si chaque terme est plus grosse que son prédécesseur, la somme grandira sans limite. Si chacune est plus petite que son prédécesseur, il y aura une limite, et la somme ne sera pas infinie. Dit autrement, si on divise chaque terme par son prédécesseur, et le quotient est moins que 1, la série « converge » — elle a une valeur finie. Si le quotient est plus que 1, la série « diverge grossièrement » — la valeur est infinie. Si le quotient est exactement 1, il faudra attendre la naissance d’Augustin Cauchy pour en parler plus.

On peut exprimer ça en ce qui concerne notre exemple en tant que formule :

Alors, on sait que la somme converge. La règle de d’Alembert ne nous dit pas quelle est la somme finale, simplement que ça existe. Je vous dirai tout simplement que le résultat final est environ 0,921.

Peut-être que ça vous semble un truc plutôt évident — si la formule baisse à chaque fois, elle ne pousse pas à l’infini ; sinon, elle pousse sans limite. Mais pour l’analyse, il ne suffit pas de dire « c’est évident » ; il faut être rigoureux. Et on ne trouve pas ce résultat chez les grecs, ni les romains, ni les allemands non plus. (Le suisse Euler l’a probablement découvert en dormant et l’a cru trop évident pour écrire, mais il était le plus grand mathématicien de l’Histoire.) Il fallait attendre Jean d’Alembert.

Après avoir parlé d’André-Marie Ampère en tant que le rhodanien le meilleur connu, on continue les « Découvertes françaises » par expliquant un peu de ce qu’il a fait. Je dis « un peu » pour deux raisons. La première, c’est qu’il était un géant historique de la physique, et de parler de tous ses réalisations remplirait tout un manuel. La deuxième, c’est qu’expliquer beaucoup de ses travaux aurait besoin d’équations comme celle-ci :

Ça parle des courants dans deux conducteurs parallèles et les forces que l’un exerce sur l’autre (lien en anglais). Mais bien que j’aie réussi mon cours d’ingénieur électrique à l’université, ça fait la moitié de ma vie, dans une autre langue, et pour être complètement honnête je l’y ai mis pour faire peur plutôt qu’éclaircir. Ce n’est pas un blog de maths avancés.

Mais on va en discuter d’une manière plus intuitive, moins formelle, en suivant une idée liée d’Ampère. Vous avez sûrement remarqué dans la formule en haut qu’il y a des x. Ça veut dire multiplication, bien sûr, mais d’une forme très particulière, une liée avec les angles droits. Et c’est à partir de ça que l’on appréciera la génie d’Ampère.

On parle donc de la « règle de la main droite ». Je vais vous dire très franchement que l’article sur Wikipédia est plutôt inutile par comparaison avec celui de Wikipedia en anglais. Ça arrive malheureusement trop souvent avec les articles scientifiques. (Les potins de célébrités, par contre, sont aussi — même encore plus — détaillés qu’en anglais ; vous mettez vos priorités dans le bon ordre.)

C’est quoi la règle de la main droite ? C’est facile à comprendre si on regarde deux diagrammes, les deux venant de Wikipedia :

Quand un courant passe tout dans le fil, ça crée un champ magnétique. Et le sens du champ est donné par la position des doigts. Vous noterez qu’en ce cas, le champ magnétique tourne autour du fil.

Mais on peut imaginer un autre cas, où le fil est tordu autour de quelque chose. On appelle cette configuration un solénoïde. Qu’est-ce qui arrive ?

Cette fois, c’est le courant qui tourne, et le champ magnétique point dans le sens du pouce. Peut-être que vous pouvez penser à une application de cette découverte. Par exemple, si on mettait une aiguille en présence du fil tout droit, l’aiguille tournerait, n’est-ce pas ? Et si la puissance du champ magnétique changeait avec la quantité du courant…peut-être que l’on pourrait l’utiliser pour signaler quelque chose dans un code ? Peut-être un code binaire, éteint ou allumé, ce qui changerait la position de l’aiguille ?

Félicitations, on vient d’inventer le télégraphe. Mais avant de féliciter M. Ampère pour être le seul et vrai inventeur du télégraphe, notez qu’il y a au moins deux façons de recevoir le signal suggérées par les diagrammes en haut. Avec un solénoïde, on pourrait faire une sonnerie, exactement ce qui se passe quand on sonne à votre porte. (Ne parlez pas du « Ring » d’Amazon, je parle évidemment de comment ça marchait jusqu’à il y a des années.) Cette autre façon est ce que l’on appelle un télégraphe armature, et c’était ce qu’a fait M. Morse. Mais même lui n’était pas « L’ » inventeur, parce qu’il y avait plusieurs idées développées en même temps partout en Europe (Cooke et Wheatstone, Gauss et Weber, Schilling).

Pourtant, tous ces télégraphes dépendent de la même théorie d’électromagnétisme, et on doit notre compréhension de la relation des courants aux champs magnétiques à André-Marie Ampère. C’est à cause de cette découverte française que l’unité pour mesurer l’intensité de courant s’appelle l’ampère.

Avant de quitter les Pyrénées-Atlantiques, on va parler d’une autre découverte française. Cette fois, c’est Frédéric Bastiat, né à Bayonne, et le coût d’opportunité, l’une des idées les plus importantes de l’histoire des études économiques. En particulier, on va parler de ça par le moyen d’où j’ai entendu parler de lui, son essai « Ce qu’on voit et ce qu’on ne voit pas ».

Commençons avec, à mon avis, le meilleur paragraphe jamais écrit par un économiste :

Avez-vous jamais été témoin de la fureur du bon bourgeois Jacques Bonhomme, quand son fils terrible est parvenu à casser un carreau de vitre ? Si vous avez assisté à ce spectacle, à coup sûr vous aurez aussi constaté que tous les assistants, fussent-ils trente, semblent s’être donné le mot pour offrir au propriétaire infortuné cette consolation uniforme : « À quelque chose malheur est bon. De tels accidents font aller l’industrie. Il faut que tout le monde vive. Que deviendraient les vitriers, si l’on ne cassait jamais de vitres ? »

Avec cette histoire, Bastiat procède à distinguer deux cas, suivant son titre. D’abord il y a ce qu’on voit :

Le vitrier va venir, il fera besogne, touchera six francs, se frottera les mains et bénira dans son cœur l’enfant terrible.

On pourrait en conclure que cette destruction est donc une bonne chose, surtout si on écoute des économistes autrichiens qui parlent de « destruction créatrice » (les autrichiens étant plutôt experts en cette matière). Bon, en fait M. Schumpeter parlait de tout autre chose, le remplacement d’une technologie par une autre, mais je n’allais pas rater cette opportunité.

De toute façon, si détruire des choses était en fait rentable, il serait logique de tout détruire et le remplacer. Mais Bastiat nous explique pourquoi cette idée n’a aucun sens :

On ne voit pas que, puisque notre bourgeois a dépensé six francs à une chose, il ne pourra plus les dépenser à une autre. On ne voit pas que s’il n’eût pas eu de vitre à remplacer, il eût remplacé, par exemple, ses souliers éculés ou mis un livre de plus dans sa bibliothèque. Bref, il aurait fait de ses six francs un emploi quelconque qu’il ne fera pas.

Ce qu’on voit, grâce à ses exemples, est l’idée que chaque consommation n’est pas seulement une question de ce qu’on achète, mais si c’est la meilleure utilisation. J’emprunterai un autre exemple de Wikipedia en anglais pour expliquer comment on peut calculer ce coût.

Imaginons que l’on gagne 80 000 € l’année. Mais on déteste son chef et veut travailler pour soi-même. On calcule que l’on pourrait facturer 60 000 € aux clients, et se paye 20 000 € en dépensant 30 000 € pour opérer l’entreprise. Le « profit comptable » est donc 60 000 – 20 000 – 30 000 = 10 000 €. Voilà, c’est plus que zéro et c’est donc une bonne idée, non ?

En fait, non. Parce qu’avant, on gagne 60 000 € moins que ce que l’on aurait pu gagner en travaillant pour le saligaud. Et si on soustrait 60 000 de nos comptes personnels en haut, au lieu de gagner 10 000 €, on perd 50 000 €. C’est ce que l’on ne voyait pas avant de commencer la nouvelle entreprise. Moi, je vois un type qui a gravement raté ce calcul en lançant sa propre entreprise à chaque fois où je me regarde dans un miroir. Ai-je mentionné que Bastiat est l’un de mes héros ?

Notre but ici n’est pas de considérer tous les jeux que les comptables ont inventés pour estimer le coût d’opportunité. C’est apprécier le génie de cette idée simple, née dans les Pyrénées-Atlantiques, qui est devenue l’une des considérations les plus importantes dans chaque plan d’affaires partout au monde — avant de se lancer dans une entreprise, il faut vraiment savoir ce que l’on ne voit pas.

Avec cet article, on lance une nouvelle catégorie, « Les découvertes françaises ». J’expliquerai tout avec la prochaine balado, mais je me doute que vous aurez déjà compris.

Avant de quitter le Puy-de-Dôme, je voulais écrire sur une pensée de son plus célèbre fils, Blaise Pascal. Je parle de son fameux pari. J’ai des sentiments mitigés quant à même évoquer le sujet, pour deux raisons. Numéro 1 « avec une balle » (« with a bullet »), comme on dit en anglais, c’est que je suis bien au courant que parler de sujets religieux est un faux pas en France. Exactement deux francophones m’ont demandé ce que je crois pendant ces 3 dernières années, ce qui me dit plus que n’importe quelle autre preuve. Disons simplement qu’il y a des indices par ici et par là le long du blog. Mais numéro 2, quel que je croie, ce blog n’est pas ici pour faire polémique… bon, pas trop souvent. 4 articles de presque 850 ? Sans en venir aux injures ? Je l’assume.

Alors, le pari de Pascal. Ça m’est arrivé dans l’esprit à cause de quelque chose dans la vraie vie il y a 3 semaines. Mais d’abord, qu’est-ce que c’est que le pari ? Pascal était philosophe, et voulait convaincre ceux en dehors de l’Église que même s’ils ne croyaient pas eux-mêmes, il valait le coup de faire un effort. Pour comprendre son argument, il faut que l’on apprenne l’idée de « valeur attendue ». Bien que je parle de cette idée dans le cadre d’une erreur, c’était un pas en avant important pour beaucoup de sujets, dont les finances et la gestion des risques.

C’est une idée très simple. Il faut savoir deux choses : la probabilité d’un événement, et ce que l’on attend à gagner s’il arrive. La valeur est le produit de multiplier ces choses. Par exemple, la valeur minimum de la loterie « Powerball » aux États-Unis est 20M $ ; quand on gagne, c’est la valeur du prix au prochain tirage au sort. Et la probabilité de la gagner, c’est 1 sur 292 201 338. La valeur attendue d’un billet est donc 20 000 000 $/292 201 338, ou 0,07 $. Pourtant les billets coûtent 2 $. C’est pourquoi je joue à la loterie seulement si le prix hausse au moins dix fois, à 200M $. La valeur attendue du billet ne s’approche presque jamais de ce qu’il coûte, mais je préfère de perdre 1,30 $ plutôt que 1,93 $. (En fait, je perds presque toujours 2 $, mais laissez tomber. C’est la valeur attendue, pas arrivée.)

Certains d’entre vous, plus doués en maths, me diront que 0,07 $ est une borne inférieure car il y a d’autres prix que l’on peut gagner, aussi plus probables. Évidemment, je le sais. Merci de ne pas compliquer l’exposition.

Pascal nous demande de considérer le résultat d’un pari sur l’existence de Dieu : soit Il existe, soit pas. Avec 2 états de réalité possibles — vous avez raison ou vous vous trompez — il y a 4 résultats possibles. J’emprunte ce tableau à Wikipédia:

Dans les cas où Dieu n’existe pas, les gains et les pertes sont limités à ce que vous arrive dans la vie ; ils sont finis. Il n’est pas vraiment important de les calculer de façon exacte. Ce qui compte sont les cas où Dieu existe et les gains et pertes deviennent illimités. Évidemment, l’un des deux est positif, et l’autre est négatif. Pascal vous dirait donc que cette analyse des risques indique qu’il vous faudrait faire un effort d’être croyant, parce que ça évitera une perte inacceptable contre 3 gains qui sont tous préférables. Oui, dans un des trois, on parie contre et a raison, mais on exclut ce cas de nos choix, car si ça ne va pas, on va dans le San Bernardino (maison de mon ancienne belle-famille).

Pourtant, même les croyants n’aiment pas souvent cet argument. Mettre à côté la plainte que l’on pourrait parier sur le mauvais dieu. C’était évident à Pascal que les cultes grecques et nordiques sont disparues à cause d’être fausses. Laplace, un grand mathématicien, avait l’avis (lien en anglais) que Pascal avait choisi la mauvaise valeur, que plus le gain est grand, moins la probabilité que le gain soit réel. (Ça implique, à tort, qu’un dieu que ne promet rien existe presque certainement.) Mais il y aussi des plaintes (lien en anglais) que la croyance n’est pas un choix — si je vous paye à croire que le soleil est bleu, vous verrez quand même la vérité, et rien n’aura changé. Ou que c’est immoral de faire un tel choix simplement pour le gain.

Mais les problèmes viennent en général du fait que l’une des valeurs est infinie. La méthode elle-même est solide. Il y a 3 semaines, on a menacé sur TikTok de faire quelque chose d’horrible à l’école de ma fille la Saint-Valentin, sans préciser quoi exactement. J’ai en fait construit le même tableau :

C’est bien évident — même sans connaître les probabilités exactes — qu’il n’y a aucun gain, et deux pertes, et l’une est bien pire que l’autre. Je l’ai donc gardée à la maison, il n’y a pas eu d’attaque, et j’ai reçu un SMS impoli exactement comme prévu. Évidemment, dans le monde des finances, il faut estimer les coûts plus exactement, et j’ai sauté par-dessus de cette complication. Mais la méthode est la même, et l’idée de valeur attendue est donc une idée de très grande valeur. Peut-être infinie.