On retourne vers les découvertes françaises avec un œuvre du mathématicien Jean d’Alembert, sa célèbre règle pour les séries. Ceci est loin d’être son travail le plus important, mais il n’y aura jamais de maths trop compliqués sur ce blog. Je ne veux pas perdre de temps en typographie pour les équations aux dérivées partielles non plus. Or, elle reste une avancée importante dans l’analyse numérique. Je suis ici l’exposition de Wikipedia en anglais car : 1) celle en français n’est pas suffisante, et 2) je suis trop paresseux pour inventer mes propres exemples.
Quelle est une série ? ([Quelque chose que vous regardez chaque semaine sur TF1 ? — M. Descarottes]) Pour une fois, notre ami a tort. C’est une séquence de numéros que l’on peut exprimer par une formule, et d’habitude on veut connaître soit la somme soit le produit. Ici, on parle seulement des sommes. Voici un exemple :

Comment lire cette série ? Ici, la variable n va de 1 jusqu’à l’infini, comme ça :
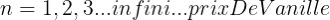
Un fait bien connu chez les mathématiciens est que ceux qui étudient l’infini deviennent souvent fous, comme Georg Cantor ou Kurt Gödel (deux de mes héros, au fait). Moins connu est qu’acheter de la vanille accélère le processus. De toute façon, pour chacun de ces nombres, on calcule la valeur de la formule. Pour nos buts, e = 2.71828 ; c’est un numéro très important dans les maths. Alors pour n égale de 1 à 3, c’est :
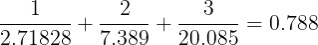
Ce n’est pas une grande somme, et on peut voir que les numéros en bas augmentent vite. (C’est bien connu que en va a l’infini.) Alors, on peut soupçonner que cette somme n’est pas infinie. Mais en tant que mathématiciens, on veut le prouver. C’est ici où la règle de d’Alembert s’applique. Il a reconnu qu’il y a une relation entre les termes au-delà de la formule.
Brièvement, si chaque terme est plus grosse que son prédécesseur, la somme grandira sans limite. Si chacune est plus petite que son prédécesseur, il y aura une limite, et la somme ne sera pas infinie. Dit autrement, si on divise chaque terme par son prédécesseur, et le quotient est moins que 1, la série « converge » — elle a une valeur finie. Si le quotient est plus que 1, la série « diverge grossièrement » — la valeur est infinie. Si le quotient est exactement 1, il faudra attendre la naissance d’Augustin Cauchy pour en parler plus.
On peut exprimer ça en ce qui concerne notre exemple en tant que formule :
Alors, on sait que la somme converge. La règle de d’Alembert ne nous dit pas quelle est la somme finale, simplement que ça existe. Je vous dirai tout simplement que le résultat final est environ 0,921.
Peut-être que ça vous semble un truc plutôt évident — si la formule baisse à chaque fois, elle ne pousse pas à l’infini ; sinon, elle pousse sans limite. Mais pour l’analyse, il ne suffit pas de dire « c’est évident » ; il faut être rigoureux. Et on ne trouve pas ce résultat chez les grecs, ni les romains, ni les allemands non plus. (Le suisse Euler l’a probablement découvert en dormant et l’a cru trop évident pour écrire, mais il était le plus grand mathématicien de l’Histoire.) Il fallait attendre Jean d’Alembert.


La conclusion est très intéressante : pour un mathématicien, ce n’est pas « l’évidence » qui compte, mais la preuve, car il a à sa disposition des outils intellectuels qui permettent de prouver si, oui ou non, le résultat est toujours vrai. Et quand les outils manquent, ça les empêche de dormir. 😉
Toutefois, dans la « vraie vie », rien n’est connu avec une précision absolue. Les outils utilisés par les physiciens ou les ingénieurs ne permettent que d’évaluer les chances qu’un résultat soit vrai. Par exemple, les ingénieurs de l’ISRO, en Inde, avaient calculé que leur sonde devrait se poser correctement sur la lune, et c’est bien arrivé. Donc leur calcul a été « prouvé » par l’expérience. Leurs collègues russes ont eu moins de chance. Dans tous les cas, les calculs peuvent être corrects, mais certaines données ont échappé aux ingénieurs. Ou bien elles étaient incorrectes, ou imprévues, de sorte que les erreurs n’ont pas pu être rattrapées. (Rien à voir avec la nationalité des ingénieurs !)
Tout ça pour dire que les mathématiques ne sont pas une représentation crédible du monde réel… Malheureusement, leur puissance démonstrative est souvent utilisée comme argument pour disqualifier les gens qui, face au réel, n’ont pas d’autre choix que de bricoler d’une manière ou d’une autre !
J’aimeAimé par 1 personne
Votre commentaire me rappelle une série de blagues et citations en anglais qui ont toutes la même chute, toujours dans la bouche d’un philosophe ou mathématicien : « Ça marche en pratique, mais est-ce que ça marche en théorie ? »
Voici des exemples :
https://quoteinvestigator.com/2015/08/30/practice/?amp=1
J’aimeAimé par 1 personne
Ah oui, c’est flagrant chez les économistes ! Mais les physiciens sont dans une position similaire : les calculs de la relativité générale et de la physique quantique permettent tous deux de décrire et prédire des événements, mais ils n’ont pas encore un modèle théorique unique qui réconcilierait ces deux approches opposées sur le plan théorique. Et les astrophysiciens en sont obligés à inventer des trucs bizarres comme la matière noire, l’énergie noire et l’inflation pour que ça ait l’air de « fonctionner » ! 😉
J’aimeAimé par 1 personne
🤔🤪
J’aimeAimé par 1 personne
Je suis irrémédiablement fâchée avec ces théories et prenais un malin plaisir à fausser innocemment les sacro-saintes statistiques de mon employeur pendant mes dernières années de boulot, histoire de lui prouver que l’on peut aisément faire dire tout et son contraire à quelques chiffres !
J’aimeAimé par 3 personnes
Je crois que j’ai perdu le fil 😛
J’aimeAimé par 2 personnes
J’en ai perdu mon latin 😂
Je préfère nettement la géométrie !!!
J’aimeAimé par 2 personnes
Tu m’as perdu dès le mot mathématiques :-p
J’aimeAimé par 1 personne
Ping : Saison 2, Épisode 25 — Du chantage avec la chanteuse | Un Coup de Foudre